Senior
Zodpovězeno: 0 z 15 otázek
Body za tuto otázku
Správná odpověď: +9 bodů
Špatná odpověď: -3 body
Nechci odpovídat: 0 bodů Hotovo - ukončit test Nápověda

Cestovní agentura nabízí těchto 10 zájezdů (viz tabulku).
Na co se má pracovník agentury zeptat zákazníka, aby mu mohl jednoznačně nabídnout zájezd podle jeho přání?
Doktor Cooper vytvořil dva kreslicí roboty, kteří mohou vykonávat následující příkazy:
Dr. Cooper položil roboty na zem a každému poslal tři příkazy:
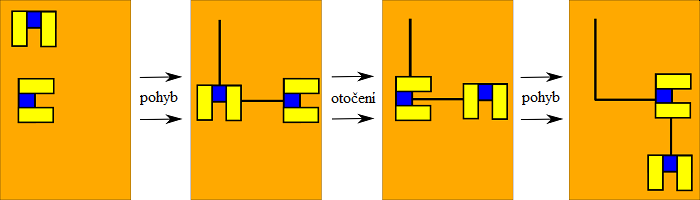
Dr. Cooper si všiml, že jeden robot si vyložil příkaz otočení jako otočku o 90 stupňů doprava, ale druhý robot si jej vyložil jako otočku o 90 stupňů doleva.
Poté dr. Cooper vyzkoušel kreslení více obrázků tak, že umístil oba roboty pokaždé na jiná místa na podlaze.
Robotům dal vždy sadu příkazů pohyb-otočení-pohyb-otočení, ... dokud nevznikl obrazec.
Také je důležité připomenout, že roboty nemohou být ve stejný čas na stejném místě.
Který z obrázků NEMOHL být nakreslen těmito dvěma roboty?
Australští farmáři v minulosti sklízeli bavlnu ručně a vozili ji do společného skladu. Aby měli přehled, psali na tabuli u vchodu, kolik žoků bavlny je uvnitř.
Zkoušeli i takovýto postup:
Na začátku sklizně byl sklad prázdný a číslo na tabuli byla 0. Potom 10 farmářů přivezlo každý jeden žok bavlny v tomto pořadí:
Č1 Č2 P1 Č3 Č4 P2 P3 Č5 P4 Č6 P5 Č7 Č8 Č9 Č10 P6 P7 P8 P9 P10
V zápisu např. Č4 znamená, že farmář č. 4 přečetl číslo, zatímco P4 znamená, že farmář č. 4 napsal na tabuli nové číslo. Pozor, číslo v zápisu neznamená číslo, které farmář napsal.
Jaké číslo bylo napsáno na tabuli na konci sklizně?
Pošťák má doručit poštu do všech pěti domů u dlouhé silnice. Domy jdou za sebou a jsou od sebe vzdáleny 1 km. Pošťák dostává zaplaceno za ušlou vzdálenost od prvního k poslednímu domu, který s poštou navštíví. Snaží se tedy nachodit co nejvíce kilometrů.
Může si zvolit, v jakém pořadí domy navštíví, v jakémkoliv domě může začít i skončit. Má doručit poštu právě jednou do každého domu, a po každém doručení musí jít přímo k dalšímu domu v pořadí, které si zvolil.
 |
 |
 |
 |
 |
| 1 | 2 | 3 | 4 | 5 |
Kolik nanejvýš kilometrů může pošťák ujít od prvního do posledního doručení?
Každý pátek si šest špiónů mezi sebou předává veškeré informace, které během týdne nashromáždili. Špión smí být v jednu chvíli viděn vždy pouze s jedním dalším špiónem, aby neriskoval odhalení. Musejí tedy provést několik kol schůzek, kde se setkávají vždy v párech a dělí se o veškeré informace, které v tu chvíli mají.
Skupina šesti špiónů potřebuje pouze tři kola, aby si navzájem předala všechna tajemství: před první schůzkou má každý špión jeden kousek informace (špión číslo 1 má informaci "a", špión číslo 2 má informace "b", atd.). V prvním kole se setkají špióni 1 a 2 a vymění si informace, tzn. že oba nyní mají informaci "ab". Diagram pomocí čar znázorňuje, jak se postupně v jednotlivých kolech špióni setkávají, a také nám ukazuje, jaké části informace všichni mají. Po třech kolech schůzek jsou všechny informace předány.

Po mezinárodním incidentu jeden ze špiónů přestal tyto schůzky navštěvovat. Jaký je minimální počet kol schůzek potřebných k tomu, aby si zbývajících 5 špiónů předalo veškeré informace?
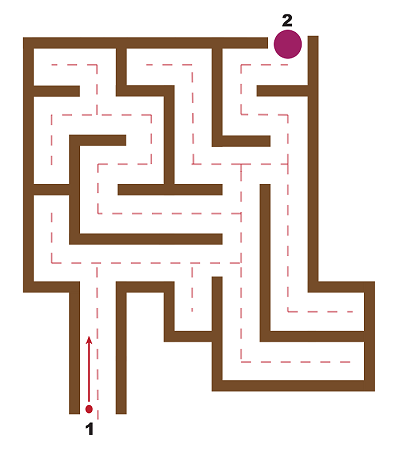
 Apu, Bart, Homer a Maggie jsou roboti, postavení studenty při informatice k procházení bludištěm. Vstoupí vchodem (1) a snaží se dostat k východu (2) - viz plánek dole.
Apu, Bart, Homer a Maggie jsou roboti, postavení studenty při informatice k procházení bludištěm. Vstoupí vchodem (1) a snaží se dostat k východu (2) - viz plánek dole.
Každý z robotů má svá pravidla (program) k nalezení východu. Opakovaně používají svá pravidla, dokud nedosáhnou východu.
Tabulka popisuje pravidla pro každého robota a ukazuje situace v malých bludištích, ve kterých roboti svá pravidla vyzkoušeli:
|
Apu:
|
Když přede mnou není zeď, jdu rovně.
Když přede mnou je zeď, zatočím doprava.
|
|
|
Bart:
|
Když nalevo není zeď, zatočím doleva a jdu rovně.
Jinak, když přede mnou je zeď, zatočím doprava.
Jinak, když přede mnou není zeď, jdu rovně.
|
|
| Homer: |
Když přede mnou není zeď, jdu rovně.
Když přede mnou je zeď, zatočím doprava a pak jdu rovně, dokud nenarazím na jinou zeď. U ní zatočím doleva a pak pokračuji rovně.
|
|
| Maggie: |
Když přede mnou není zeď, jdu rovně.
Když přede mnou je zeď, zatočím doleva.
|
|
Kdo z robotů podle svých pravidel dojde k východu z tohoto bludiště?
 Integrovaný obvod obsahuje mnoho kontaktů uspořádaných do mřížky (znázorněné na obrázku jako body). Některé jsou již propojeny pomocí segmentů (znázorněných jako úsečky). Segmenty spojují vždy sousední kontakty, svisle či vodorovně. Nyní chceme propojit černé kontakty v rozích integrovaného obvodu, ovšem bez dotyku s již rozmístěnými segmenty.
Integrovaný obvod obsahuje mnoho kontaktů uspořádaných do mřížky (znázorněné na obrázku jako body). Některé jsou již propojeny pomocí segmentů (znázorněných jako úsečky). Segmenty spojují vždy sousední kontakty, svisle či vodorovně. Nyní chceme propojit černé kontakty v rozích integrovaného obvodu, ovšem bez dotyku s již rozmístěnými segmenty.
Kolik nejméně segmentů je třeba k propojení černých kontaktů?
Studenti školy pojedou na exkurzi. Učitel vybírá studenty, kteří se jí zúčastní, podle sociologického průzkumu vztahů mezi nimi. Průzkum dává dva druhy pravidel:
Ve třídě je 9 studentů, kteří projevili o exkurzi zájem: Anna, Bořek, Cilka, David, Eva, Gusta, Helena, Jiří a Lukáš. Učitel sám vybere prvních pět studentů, kteří pojedou na exkurzi: Annu, Cilku, Evu, Gustu a Helenu. Podle výsledků průzkumu platí ještě:
Kolik studentů nakonec půjde na exkurzi?
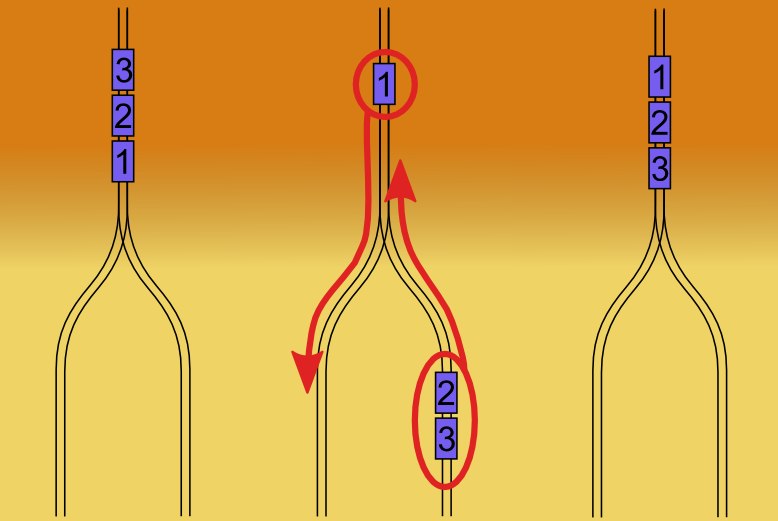
 Na nádraží stojí na kopečku tři motorové vozy (na obrázku dole vlevo) a mají se posunováním poskládat do opačného pořadí (na obrázku dole vpravo).
Na nádraží stojí na kopečku tři motorové vozy (na obrázku dole vlevo) a mají se posunováním poskládat do opačného pořadí (na obrázku dole vpravo).
Posunovač má pod kopečkem k dispozici dvě koleje a může provádět tyto činnosti (na obrázku dole uprostřed):
1. Spuštění: Nechá sjet jeden vůz z kopečka do libovolné ze dvou kolejí.
2. Vytažení: Nechá vytáhnout všechny motorové vozy z jedné ze dvou kolejí nahoru na kopeček (je-li na koleji více vozů, spojí se a vyjedou najednou).
Spuštění vozu je velmi snadné, stačí do vozu strčit a on sjede z kopce sám.
Vytažení je náročná a drahá činnost, protože jeden z vozů musí zapnout motor a vytáhnout sebe (a případně ostatní) na kopeček. Proto se posunovač snaží co nejméněkrát vytahovat.
Kolikrát nejméně musí posunovač provést vytažení, aby vozy uspořádal do opačného pořadí?
Lukostřelec Robin chce svým šípem trefit terč ležící na zemi (obrázek). Je schopen zamířit lukem tak, aby šíp padl podle jeho přání kamkoliv mezi značky 0 m a 10 m. Polohu terče nezná, ale ví, že terč má velikost 50 cm a leží pořád na stejném místě. Po každém výstřelu mu jeho pomocník John ohlásí, jestli terč trefil, nebo jestli střelil do země před terč, nebo za terč.
Jaký nejmenší počet pokusů Robin potřebuje, aby si byl jist, že trefí terč nezávisle na tom, kde terč leží?

Na místě, kde je v řece množství ostrůvků, se elektrárenská firma rozhodla postavit přehradu, protože je levnější stavět více menších hrází než jednu velikou.
Inženýři provedli průzkum podloží, hloubky a proudu v různých místech a spočítali, kolik milionů eur by na těchto místech stálo postavit hráz (viz obrázek).
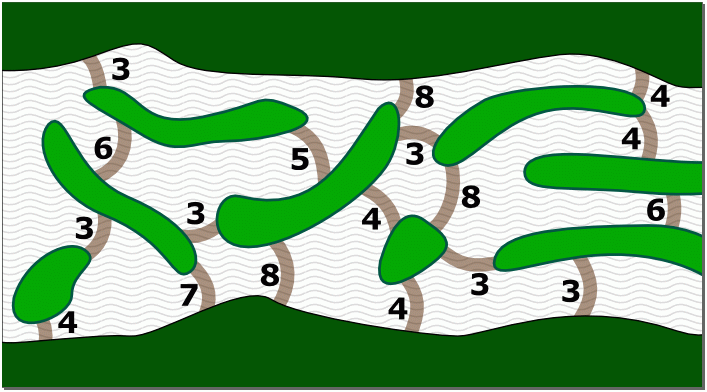
Firma chce přehradu postavit co nejlevněji. Kolik nejméně může stát postavení přehrady přes celou řeku?

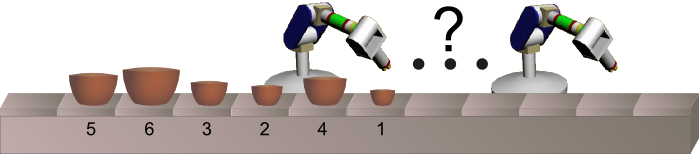
V továrně mají výrobní linku na výrobu sady misek, které jde složit do sebe. Na konci linky stojí stroj, který misky kompletuje. K tomu potřebuje, aby byly položeny na pás ve správném pořadí (horní obrázek).
Na pásu však misky přicházejí promíchány, proto u pásu stojí robot, který kontroluje velikost procházejících misek, a může dvě vedle sebe stojící misky navzájem vyměnit.
Na následujících obrázcích je vidět příklad, jak takový robot pracuje, když kolem něj prochází sada neuspořádaných misek. Šipky ukazují, které dvě misky robot v příštím kroku vymění.

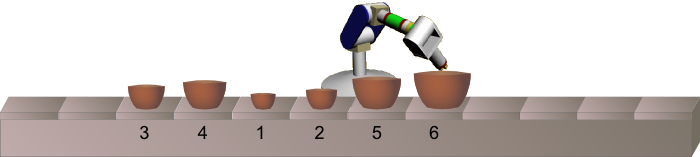

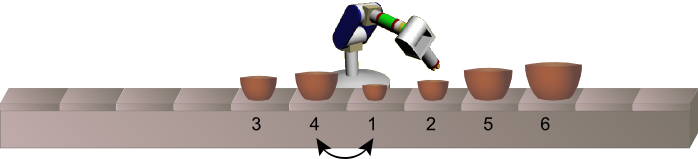
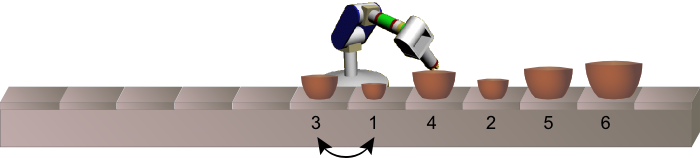
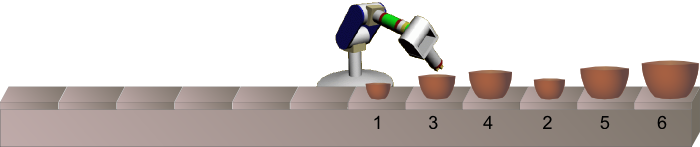
Jeden robot ovšem nepřerovná všechny misky tak, aby stály ve správném pořadí. Proto majitel musí koupit takových robotů více a rozestavět je za sebou podél pásu.
Kolik robotů je třeba, aby misky na obrázku dole srovnaly do správného pořadí? Zapiš číslicí.
Firma Ohýnek připravuje speciální ohňostroje na městské slavnosti. Aby byl každý ohňostroj jedinečný, vytváří v něm posloupností výstřelů symbolizaci všech znaků v městském erbu.
Symboly, které v erbech firma často používá, jsou lev, orlice, kůň, růže a hradby. Pro ně vytvořila zvláštní kódy (viz tabulku).
| SYMBOL | KÓD | ........................ | SYMBOL | KÓD |
| lev |   |
růže |  |
|
| orlice |    |
hradby |   |
|
| kůň |    |
Například, pokud je v erbu orlice a růže, ohňostroj bude vypadat takto:




Kolik různých městských erbů může vyjadřovat následující ohňostroj?








Kája si naprogramoval jednoduchý stroj, aby šifroval jeho tajné zprávy kamarádům.
Obrázek ukazuje, jak jeho stroj šifruje slovo KOSTKY.

Které slovo bylo zašifrováno do slova OFDUTPO?
 Kreslicí robot jezdí po dlaždicích a obarví každé pole, na které vstoupí. Dá se ovládat programem:
Kreslicí robot jezdí po dlaždicích a obarví každé pole, na které vstoupí. Dá se ovládat programem:
| Program | Robot provede: |
| 4J | - robot jede o 4 pole na jih od místa, kde stojí |
| 3V1Z | - robot jede o 3 pole na východ a pak o 1 pole na západ |
| 2J3VS | - robot jede o 2 pole na jih, pak o 3 pole na východ a pak o 1 pole na sever |
| 4(3JV4S) | - robot vykoná čtyřikrát příkazy v závorce |
Napiš program, aby robot obarvil šedý ornament.
Do řádku napiš program, po stisknutí tlačítka Uložit odpověď se vykreslí obrázek. Můžeš zkoušet vícekrát.
Na začátku stojí robot v zeleném poli.
Pole, která zezelenají, robot vybarvil správně, červená pole nesprávně.
Maximální délka programu může být 10 znaků. Mohou se psát mezery, ale počítají se do počtu znaků.
Při psaní programu není povoleno vnořování závorek: (())
Informace k testu
- Své odpovědi můžeš během testu změnit, kolikrát budeš chtít.- Pokud chceš ukončit test před vypršením časového limitu, stiskni tlačítko Hotovo - Ukončit testování.
- Po skončení testu se okamžitě dozvíš výsledek.
- Pokud bys během testování potřeboval pokračovat v testu na jiném počítači, budeš potřebovat své heslo soutěžícího.