B.Challenge
Zodpovězeno: 0 z 15 otázek
Body za tuto otázku
Správná odpověď: +9 bodů
Špatná odpověď: -3 body
Nechci odpovídat: 0 bodů Hotovo - ukončit test Nápověda
Společnost EL Trička vyrábí potisky na trička na základě kombinace elips. Na jejich webových stránkách si můžeš navrhnout vlastní potisk buď přidáním elipsy dané velikosti s jakoukoliv orientací, nebo použitím speciálních pravidel pro kombinaci elips. Existují tři speciální pravidla A + B, A – B a A * B.
Pravidlo A + B je definováno tak, že se nejdříve vytiskne elipsa A a poté elipsa B, která může (ale nemusí) překrývat elipsu A. Například pokud A je žlutá plná elipsa a B je bílá modře vlnkovaná elipsa, může pravidlo A + B vytvořit následující potisky:
 |
 |
 |
Všimni si však, že B + A by mohlo vypadat jinak:
 |
Pravidlo A – B je definováno jako ta část elipsy A, která není překryta elipsou B.
Pravidlo A * B je definováno jako ta část elipsy B, která překrývá elipsu A.
Pro stejně umístěné elipsy budou potisky podle těchto pravidel vypadat takto:
| A + B | A – B | B – A | A * B |
|
|
 |
 |
|
EL Trička organizuje soutěž o nejhezčí potisk měsíce. Účastníci vezmou dvě elipsy E a F, rozmístí je podle svého uvážení a aplikují na ně speciální pravidlo, které pro tento měsíc zní (E + F) – (E * F). Stejně jako u matematických operací, i zde se nejdříve vyhodnocuje obsah závorek.
Porotci soutěže si všimli, že jeden ze zaslaných návrhů neodpovídá pravidlu pro tento měsíc.
Který potisk neodpovídá pravidlu pro tento měsíc?
Na obrázku jsou grafem znázorněny jednosměrné ulice. Číslo v každém uzlu znamená nejkratší vzdálenost z S do tohoto uzlu.
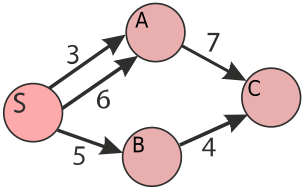
Na horním obrázku vedou z S do A dvě cesty délky 3, 6, do uzlu A bychom napsali číslo 3.
Z uzlu S do C vedou celkem 3 cesty délek 10, 13, 9. Do C bychom napsali číslo 9.
Které z následujících tvrzení o dvou tlustě ohraničených uzlech na spodním grafu je pravdivé?
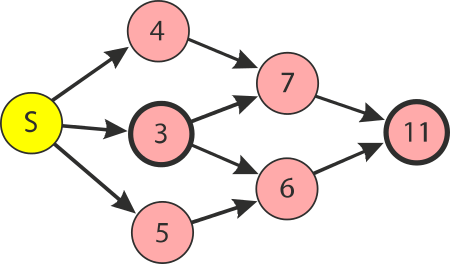
Definujeme základní operace takto:
Dále definujeme, že vzdálenost mezi dvěma řetězci je minimální počet základních operací, které umožní změnit jeden řetězec v druhý.
Příklad: vzdálenost řetězců "opice" a "kolie" je 3:
Jaká je vzdálenost řetězců "length" a "french"?
Napiš číslo.
Hotel má 5 podlaží, na každém 8 pokojů. Robot, který pokoje uklízí, pracuje podle instrukcí, které znamenají:
C - najdi nějaký neuklizený pokoj na tomto podlaží a ukliď jej
U - přesuň se o jedno podlaží výše
D - přesuň se o jedno podlaží níže
n () - zopakuj vše, co je uvedeno mezi závorkami, tolikrát, kolik je číslo n.
Např. pokud má robot uklidit dva neuklizené pokoje na tomto patře, dej mu instrukce 2(C). Jestliže má poté robot sejít o jedno podlaží níže, pak napiš 2(C) D.
Každou neděli jsou všechny pokoje neuklizené. Robot začíná úklid na 1. podlaží a také na 1. podlaží končí.
Jaká sada instrukcí je správná, aby robot uklidil všechny pokoje a přitom ani jednou neopustil těchto 5 podlaží?
Počítačový program je napsán v jazyce, jehož syntaxe x ← y + z znamená "do proměnné x dosaď součet hodnot z proměnných y, z".
Počítačový program používá tři proměnné a, b, c. Obsahuje tyto instrukce, které vykonává postupně:
b ← a
c ← a + b
a ← b – c
b ← b + a
c ← b + a
a ← c – a
Po vykonání programu byl obsah proměnných následující: a: 0, b: 0, c: –3.
Jakou hodnotu měla proměnná a na začátku, před vykonáním programu?
Zapiš číslo.
Na ostrově rostou speciální stromy. Strom typu A žije 1 rok a na konci tohoto roku vyprodukuje semínko typu B. Z něj na začátku dalšího roku vyroste strom typu B, který každým rokem vyprodukuje semínko typu A a nikdy neuhyne. Ze semínka typu A pak v dalším roce vyroste strom typu A.
Když vysadíme 1 semínko typu A, kolik semínek typu B z něj bude po 10 letech?
Napiš číslo.
Robot se umí pohybovat po čtvercové mřížce za pomocí kroků směrem na sever nebo na východ. Robotu se instrukce dávají za pomoci diagramů (jako ten na obrázku) – říkají, jakou trasou (tedy sérií kroků na sever a kroků na východ) může robot jít.

Povolené kroky robot zjistí v diagramu:
Například, pokud by se robot řídil diagramem výše, tak začíná krokem na sever a pak vykonává střídavě kroky na východ a na sever a může se zastavit pouze po kroku na sever. To znamená, že například SVSVSVS, SVS, nebo SVSVSVSVSVSVS jsou povolené trasy, ale SVSSV, SVSV, nebo VSV nikoliv.
Robot se nyní řídí diagramem níže.

Kterou z následujících částí neobsahuje žádná povolená trasa robota ?
Očíslované míčky se kutálejí po rampě. Když se míček přikutálí k díře, ve které je místo, spadne do ní. Není-li v díře místo, kutálí se dál. Poté, co vytáhneme kolíček na dně díry, pérko vytlačí míčky z díry a ty se kutálí dál. Jejich pořadí se ale patrně změní.
Zde je příklad:
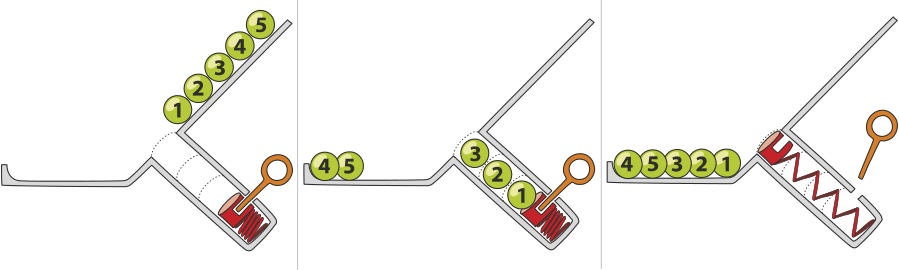
| na začátku | poté, co se míčky zastavily | na konci po uvolnění kolíčku |
Úloha pro tebe:
10 míčků se kutálí po rampě. Tři díry A, B, C mají prostor pro jeden, dva, tři míčky. Pokaždé, když se všechny míčky zastaví, vytáhneme kolíček. Pružina vystřelí, pak se hned zase natáhne a my zastrčíme kolíček. Kolíčky vytahujeme opakovaně v pořadí A, B, C tak dlouho, dokud nejsou všechny míčky dole.

Jaké bude pořadí míčků na konci? Zapiš číslicemi bez mezer (např. 1526480379)
Pavel vytvořil černobílý obrázek o velikosti 6 x 4 body. Nepoužil žádnou komprimaci, přesto v paměti počítače stačily na uchování jeho obrazových dat 3 bajty.
Erika nakreslila v bitmapovém editoru vlajku naší země (obrázek). Vlajka měla rozměry 150 x 100 bodů.
Kolik NEJMÉNĚ místa v paměti počítače stačí k uchování jeho obrazových dat?
Nebereme v úvahu žádnou komprimaci dat.

Milan postavil robota, který umí poznat barvu čtverce, na kterém stojí, změnit jeho barvu a posouvat se o jeden čtverec doprava nebo doleva. Robot pracuje podle pravidel jako jsou tato:
Pravidlo  znamená: Když jsi na červeném čtverci, změň jeho barvu na zelenou a posuň se o jeden čtverec doprava.
znamená: Když jsi na červeném čtverci, změň jeho barvu na zelenou a posuň se o jeden čtverec doprava.
Pravidlo  znamená: Když jsi na červeném čtverci, změň jeho barvu na zelenou a posuň se o jeden čtverec doleva.
znamená: Když jsi na červeném čtverci, změň jeho barvu na zelenou a posuň se o jeden čtverec doleva.
Na začátku robot stojí na prvním čtverci zleva. Robot vždy nejprve zjistí barvu čtverce, na kterém stojí, najde pravidlo, které touto barvou začíná, a pak podle tohoto pravidla změní barvu čtverce a posune se. Po přesunu tuto činnost zopakuje pro čtverec, na který se přesunul, a tak pokračuje dál a dál. Když robot nenalezne vhodné pravidlo nebo se přesune mimo čtverce, zastaví se.
Robot dostal tuto řadu čtverců:

Dále dostal tato pravidla:
 |
 |
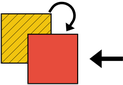 |
Jak bude řada čtverců vypadat poté, co se robot zastaví?
Robot Mysto potřebuje nalézt cestu ven z bludiště a žádá tě, abys mu s tím pomohl. Do bludiště vstupuje seshora (černý trojúhelník) a potřebuje se dostat k východu (na červený kruh). Trojúhelník ukazuje, kterým směrem je Mysto otočený. Robot dokáže pracovat pouze s následujícími třemi druhy instrukcí:
| Popojdi o jedno pole vpřed a na místě se otoč doprava. | |
| Popojdi o jedno pole vpřed a na místě se otoč doleva. | |
| Popojdi o jedno pole vpřed. |
Navíc má paměť pouze na osm instrukcí, ovšem může je opakovat, dokud nedojde do cíle (nebo nenarazí do zdi).
Jaké instrukce Mysto potřebuje, aby se dostal k východu z bludiště? Sestav instrukce do smyčky (vedle bludiště, přetáhni je myší zprava).
























Toto je klasická hádanka. Muž má převézt na druhý břeh řeky vlka, ovci a řepu. Má k dispozici loďku, na kterou se vejde pouze on a jeden další objekt. Ovšem nemůže nechat bez dozoru na jednom břehu společně vlka a ovci, protože vlk by ovci sežral. Podobně nemůže nechat spolu ovci a řepu samotné, protože by ovce řepu sežrala. Otázka této hádanky zní, jak má muž tyto tři objekty na druhou stranu řeky převézt.
Řešení této hádanky lze vyjádřit pomocí grafu (obrázek). Souřadnice objektů (vlka, ovce, řepy) může být vyjádřena číslem 0, pokud je objekt na původním břehu řeky, a číslem 1, pokud je na druhém, cílovém břehu. Hrany grafu pak znázorňují přesuny objektů mezi břehy.
Například změna souřadnic z (0,0,0) na (0,0,1) znamená, že řepa byla převezena na druhý břeh řeky, zatímco změna z (0,0,1) na (0,0,0) znamená, že řepa byla převezena zpět na původní břeh.
Nyní ovšem potřebujeme smazat "zakázané" hrany grafu. Jinak by něco mohlo sežrat něco jiného, pokud s nimi muž nebude na témže břehu řeky.
Které hrany grafu musíme odstranit?
Klikej na hrany a označ ty, které se mají odstranit.








Systém umí rozeznat digitální číslice vypadající takto:

Každá číslice je tvořena až 7 segmenty. Aby se však dala číslice rozeznat, nejsou k tomu potřeba všechny segmenty. Stačí vidět jen některé, aby se číslice dala rozeznat od ostatních.
Vyber ty segmenty, které jsou bezpodmínečně nutné k rozeznání všech číslic 0 .. 9.
Klikej na segmenty.







 V bance je řada trezorů, každý se odemyká klíčem. V prvním trezoru je uchována 1 zlatá mince, ve druhém 2 zlaté mince, ve třetím 4 a v každém dalším vždy dvojnásobek zlatých mincí (obrázek).
V bance je řada trezorů, každý se odemyká klíčem. V prvním trezoru je uchována 1 zlatá mince, ve druhém 2 zlaté mince, ve třetím 4 a v každém dalším vždy dvojnásobek zlatých mincí (obrázek).
Kolem trezorů chodí robot, který otočením klíčem trezor odemkne (pokud je zamčený) nebo zamkne (pokud je odemčený). Odemčené trezory zeleně svítí.
Např. na obrázku jsou odemčeny tři trezory s celkem 13 přístupnými mincemi.
Robot prochází kolem trezorů každou hodinu, vždy vychází od prvního trezoru. Přitom otáčí klíči podle těchto pravidel:
Uvažujme, že řada trezorů je tak dlouhá, že vždy je nějaký trezor uzamčen.
Robot chodí skoro celý týden a po každé procházce zpřístupní různý počet mincí. Během tohoto týdne nikdo mince nepřinesl ani neodnesl.
Které z následujících tvrzení je pravdivé?
Hobití klub otesánků si na slavnosti každoročně vybírá svého krále z kandidátů, kteří se spolu utkají po dvojicích turnajovým způsobem. Z každé dvojice vzejde vítěz, který postoupí do dalšího kola. Kdo vyhraje i poslední kolo (finále), je král.
O kvalitě kandidáta na krále rozhoduje pouze jeho váha a výška. O vítězi rozhodují tato složitá pravidla:Letos se hlásí 8 kandidátů. Zde jsou jejich startovní čísla, výšky a váhy. V grafu dole je vidět jejich rozlosování do dvojic.
1 = 72 cm, 60 kgDoplň do grafu všechna chybějící čísla a urči tak nového krále otesánků.
























Informace k testu
- Své odpovědi můžeš během testu změnit, kolikrát budeš chtít.- Pokud chceš ukončit test před vypršením časového limitu, stiskni tlačítko Hotovo - Ukončit testování.
- Po skončení testu se okamžitě dozvíš výsledek.
- Pokud bys během testování potřeboval pokračovat v testu na jiném počítači, budeš potřebovat své heslo soutěžícího.